Jak powiedział John Rennie, ma to związek z rozmywaniem cieni. Jednak samo to nie do końca wyjaśnia.

Zróbmy to z faktycznym rozmywaniem:

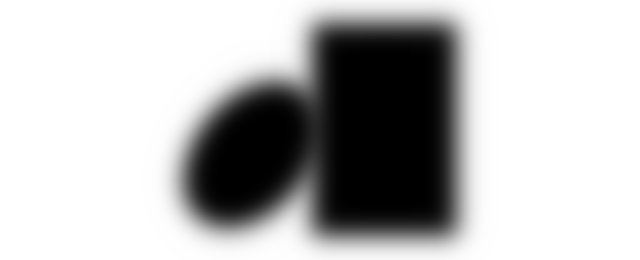
Zasymulowałem cień, rozmywając każdy kształt i pomnożenie wartości jasności ¹ . Oto plik GIMP, dzięki czemu możesz zobaczyć, jak dokładnie i przesuwać kształty wokół siebie.

Nie sądzę, żebyś powiedział, że ma miejsce jakieś zginanie, przynajmniej ja, krawędź książki nadal wygląda idealnie prosto.

Więc co się dzieje w twoim eksperymencie?

Odpowiedź nieliniowa jest odpowiedzią. W szczególności w Twoim filmie ściana oświetlona bezpośrednio słońcem jest prześwietlona, ​​tzn. Niezależnie od „dokładnej jasności” wartość piksela jest czysta biel. W przypadku ciemnych odcieni funkcja tłumienia szumów aparatu przycina wartości do czerni. Możemy to zasymulować na powyższym obrazku:

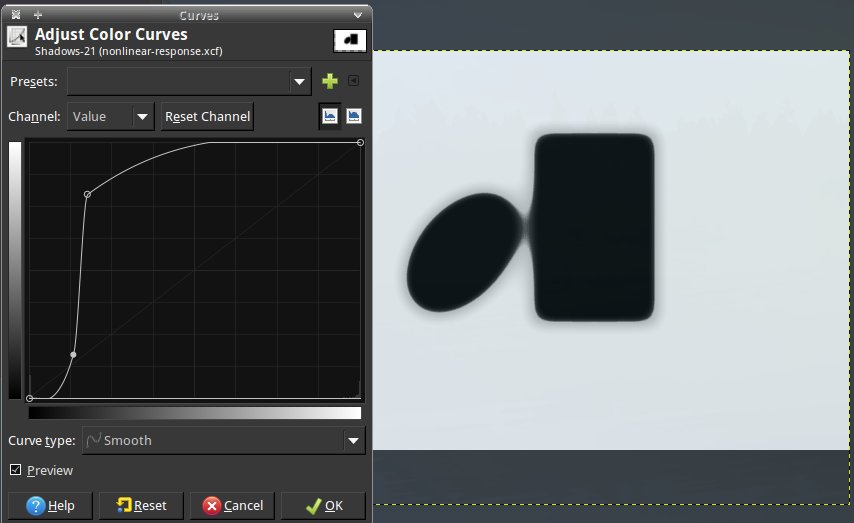
Teraz to wygląda bardzo podobnie do Twojego filmu, prawda?

Z gołymi oczami , normalnie tego nie zauważysz, ponieważ nasze oczy są w pewnym sensie wyszkolone, aby kompensować efekt, dlatego nic nie wygląda na wygięte na nieprzetworzonym obrazie. To zawodzi tylko w dość ekstremalnych warunkach oświetleniowych: prawdopodobnie większość twojego pokoju jest ciemna, a dość wąska wiązka światła zapewnia bardzo duży zakres jasności. Wtedy oczy również zachowują się zbyt nieliniowo, a mózg nie może już zrekonstruować, jak wyglądałyby kształty bez rozmycia.

Właściwie topografia jasności jest zawsze taka sama, co widać po kwantyzacji paleta kolorów:

¹ Aby poprawnie zasymulować cienie, musisz użyć splotu cały otwór, z kształtem słońca jako jądrem. Jak zauważa Ilmari Karonen, robi to istotną różnicę: splot iloczynu dwóch ostrych cieni $ A $ i $ B $ z rozmytym jądrem $ K $ wynosi

$$ \ begin {aligned} C (\ mathbf {x}) = & \ int _ {\ mathbb {R} ^ 2} \! \ mathrm {d} {\ mathbf {x '}} \: \ Bigl ( A (\ mathbf {x} - \ mathbf {x} ') \ cdot B (\ mathbf {x} - \ mathbf {x'}) \ Bigr) \ cdot K (\ mathbf {x} ') \\ = & \ mathrm {IFT} \ left (\ backslash {\ mathbf {k}} \ to \ mathrm {FT} \ Bigl (\ backslash \ mathbf {x} '\ to A (\ mathbf {x}') \ cdot B ( \ mathbf {x} ') \ Bigr) (\ mathbf {k}) \ cdot \ tilde {K} (\ mathbf {k}) \ right) (\ mathbf {x}) \ end {aligned} $$

podczas gdy oddzielne rozmycie daje

$$ \ begin {aligned} D (\ mathbf {x}) = & \ left (\ int _ {\ mathbb {R} ^ 2} \! \ mathrm {d} {\ mathbf {x '}} \: A (\ mathbf {x} - \ mathbf {x}') \ cdot K (\ mathbf {x} ') \ right) \ cdot \ int _ {\ mathbb {R} ^ 2} \! \ Mathrm {d} {\ mathbf {x '}} \: B (\ mathbf {x} - \ mathbf {x'}) \ cdot K (\ mathbf {x} ') \ \ = & \ mathrm {IFT} \ left (\ backslash {\ mathbf {k}} \ to \ tilde {A} (\ mathbf {k}) \ cdot \ tilde {K} (\ mathbf {k}) \ right) (\ mathbf {x}) \ cdot \ mathrm {IFT} \ left (\ backslash {\ mathbf {k}} \ to \ tilde {B} (\ mathbf {k}) \ cdot \ tilde {K} (\ mathbf {k}) \ right) (\ mathbf {x}). \ end {aligned} $$

Jeśli wykonamy to dla wąskiej szczeliny o szerokości $ w $ pomiędzy dwoma cieniami ( prawie szczyt Diraca), transformatę Fouriera iloczynu można przybliżyć stałą proporcjonalną do $ w $, podczas gdy $ \ mathrm {FT} $ każdego cienia pozostaje $ \ mathrm {sinc} $ - kształt, więc jeśli weźmiemy serię Taylora za wąskie nakładanie się, to pokazuje, że jasność spadnie tylko jako $ \ sqrt {w} $, tj. pozostanie jaśniejsza na bliskich odległościach, co oczywiście tłumi wybrzuszenie.

I rzeczywiście, jeśli odpowiednio rozmyjemy oba cienie razem , nawet bez żadnej nieliniowości, uzyskamy znacznie bardziej "efekt mostkowania":

Ale to nadal nie wygląda na tak „wypukłe”, jak to, co widać w Twoim filmie.

Dzieje się tak, ponieważ Słońce nie jest źródłem punktowym, więc krawędzie cieni są lekko rozmyte. Oto moja dość prymitywna próba wyjaśnienia, dlaczego tak się dzieje:

W artykule Wikipedii na temat umbra są znacznie lepsze diagramy, które wyjaśniają co się dzieje. Rozmyty kawałek na krawędzi cienia nazywa się półcieniem.

Przyczyną, dla której widzisz wybrzuszenie w miejscu, w którym cienie się zbliżają, jest półcień i fakt, że ludzkie oko nie jest zbyt dobry w radzeniu sobie z kontrastem. Gdy dwa cienie się zbliżają, ale zanim się dotkną, ich półcienie (półcienie?) Nakładają się na siebie. Oznacza to, że obszar między cieniami jest ciemniejszy niż reszta półcienia. Następuje inny dość prymitywny diagram:

To nie jest dobry diagram, ponieważ gęstość półcienia nie jest stała, ale raczej odcienie od czerni do bieli w poprzek szerokość. Jednak Google Draw nie wykonuje wypełnień gradientowych, więc utknąłem z raczej słabą reprezentacją. W każdym razie, miejmy nadzieję, powinno być oczywiste, że tam, gdzie półcienie nachodzą na siebie, przyciemniają się nawzajem, więc obszar między dwoma cieniami staje się ciemniejszy. Ponieważ oko nie radzi sobie dobrze z szerokim zakresem kontrastu, wygląda na to, że cienie wybrzuszały się względem siebie.

Uważam, że przyczyną jest dyfrakcja, jak opisano w tym artykule. Zdjęcie przedstawia podobny efekt, gdy trzymasz dwa palce blisko siebie.

Efekt czarnej kropli opisany w Sky and Telescope

Kiedy łączysz łokieć i książkę, tworzysz wzór dyfrakcyjny, jaki można zobaczyć na obraz w artykule poniżej, jaśniejsze światło pośrodku z czarnymi pasami po obu stronach. Gdy zbliżasz je jeszcze bliżej, czarne paski zbliżają się do siebie. Dlatego wydają się nagle „skakać” do siebie.

Obraz standardowego wzoru dyfrakcyjnego

Nie gwarantuję, że to jest poprawna odpowiedź, ale możesz ją praktycznie zweryfikować.

Promienie świetlne rzucające cień na twoją dłoń i twoją książkę nie są równoległe. Wypukłość cieni, gdy są blisko siebie, oznacza, że ​​oba wybrzuszone cienie pochodzą z łokcia. Tak więc w momencie, gdy łokieć znajduje się w pobliżu książki, na łokieć działają dwa źródła światła (lub takie zakrzywienie światła, że ​​na łokieć działają niezrównane promienie, powodując dwa cienie).

Myślę, że Ty też to odgadłeś. Możesz to sprawdzić, wykonując dwie czynności:

1. Otwierając okno, aby padało bezpośrednie światło. Dzięki temu dowiesz się, czy zginanie jest spowodowane przez szklane okno.
2. Zmiana wysokości książki i zgięcia łokcia. okno. Spróbuj sprawdzić, czy efekt jest obserwowany na wszystkich wysokościach.

Przypadkowo zastanawiałem się ostatnio nad podobnym efektem, gdy skupiasz wzrok na pobliskim obiekcie, powiedzmy palcu, obiekty za nim w oddali wydają się być zakrzywione / zniekształcone wokół krawędzi twojego palec. Wydaje się okropnie powiązane ...

Masz rację, że są spokrewnieni. To kolejny efekt dyfrakcji. Widzisz dyfrakcję pojedynczej krawędzi, znaną również jako efekt krawędzi noża. Tutaj jest opisująca to strona internetowa.

Światło przechodzące bardzo blisko palca jest odchylane. Odkąd zmienił się kierunek, wydaje się, że pochodzi z innego miejsca.

Wypróbuj to w pomieszczeniu, w którym jest jeden z tych wentylatorów sufitowych z czterema żarówkami. Wiele źródeł światła wytwarza wiele dobrze widocznych cieni i można zobaczyć, jak ten rodzaj zjawiska zaczyna obowiązywać. Kiedy cienie nakładają się na siebie, daje to taki wygląd i wywołuje zjawiska, o których mowa. W normalnych sytuacjach napotkanymi wieloma źródłami światła często może być światło odbijane od ścian i pobliskich obiektów, wszystko, co jest białe lub jaśniejsze. Powstające liczne cienie są tak słabe, że nie są nawet zauważalne, dopóki nie nałożą się na inne cienie. Źródła światła pod różnymi kątami wytwarzają wiele cieni. Na przykład, gdy łokieć przesuwa się w stronę książki, wiele cieni z obu obiektów nakłada się na siebie, gdzie wydają się łączyć. To, co wygląda jak krawędź cienia pojedynczego obiektu, jest krawędzią miejsca, w którym warstwy cieni nakładają się najbardziej na siebie.