Przy wysokim ciśnieniu średnia swobodna droga elektronów jest dość niska. Elektrony nie mają wystarczająco dużo czasu na przyspieszenie. Jeśli elektrony nie przyspieszają zbyt długo, nie mogą uzyskać dużej prędkości lub energii kinetycznej potrzebnej do jonizacji innych atomów.

Chociaż twój argument, że jeśli jest więcej atomów, więcej elektronów można uzyskać poprzez jonizację , ma sens, nie uwzględniasz faktu, że tylko elektrony o wysokiej energii mogą jonizować elektrony z atomów gazu . Jeśli jest zbyt wiele atomów gazu, elektrony zderzają się znacznie, zanim osiągną wystarczającą energię kinetyczną, aby zjonizować atomy. Jeśli nie możesz uzyskać ruchu dużej liczby elektronów, nie uzyskasz wystarczającego prądu.

Kiedy ciśnienie gazu jest niskie (ale nie za niskie), elektrony mają wystarczająco dużo czasu (lub odległość), aby przyspieszyć. Zanim zderzają się z atomem, uzyskali wystarczającą ilość energii kinetycznej z pola elektrycznego, aby zjonizować inne atomy. Chociaż nie ma wielu atomów, z których można uzyskać elektrony w porównaniu z gazem pod wysokim ciśnieniem, jest ich więcej niż wystarczająco, aby wytworzyć mierzalny prąd.

Jeśli ciśnienie gazu jest zbyt niskie, twoja argumentacja zaczyna działać. Nie będzie wystarczającej liczby atomów do jonizacji, a przewodnictwo spadnie.

M Szczegóły matematyczne:

$$ V_ {B} = \ frac {Bpd} {ln (Apd) - ln (ln (1 + \ frac {1} {\ gamma_ {se}}))} $$

gdzie $ V_B $ to napięcie przebicia (minimalne napięcie wymagane do zaobserwowania mierzalnego prądu), $ p $ to ciśnienie gazu, $ d $ to odległość między elektrodami, $ A $ to nasycenie jonizacji gaz, a $ \ gamma_ {se} $ jest współczynnikiem wtórnej emisji elektronów, a $ B $ jest stałą związaną z energią jonizacji.

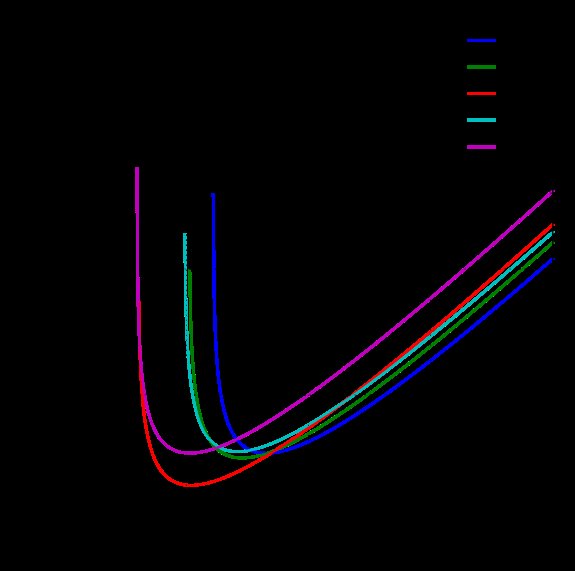
Intution:

Gdy ciśnienie jest zbyt niskie, trudno jest uzyskać znaczną liczbę elektronów do wytworzenia mierzalnego prądu.

W przypadku ciśnienia, które nie jest ani za niskie, ani za wysokie, to, jak zmienia się przewodnictwo, można zrozumieć w następujący sposób.

Jeśli swobodny elektron przechodził przez dwie elektrody z różnicą potencjałów $ V $ w doskonałej próżni, energia kinetyczna elektronu uzyskiwana przez elektron wynosi:

$$ K.E = eV $$

Niech odległość między elektrodami będzie wynosić $ L $. Jeśli elektron pokonuje odległość $ x $ (średnia swobodna droga), zanim zderzy się z atomem, energia kinetyczna uzyskana przez elektron wynosi:

$$ K.E = e (Ex) = ex \ frac {V} {L} $$

Elektron musi mieć co najmniej $ W $ (nazwijmy tę funkcję pracy) energii, aby zjonizować atom.

Jeśli musi nastąpić znaczna jonizacja, to: $$ K.E \ ge W $$

$$ ex \ frac {V} {L} \ ge W \ tag {1} $$

Średnia swobodna droga elektronu jest proporcjonalna (jeśli nie równa) do średniej swobodnej ścieżki gazu. Średnia droga swobodna gazu zmienia się w następujący sposób:

$$ \ lambda = k \ frac {T} {P} \ tag {2} $$

Zastępując równanie $ (2) $ w równaniu $ (1) $, otrzymujemy:

$$ k_1 \ frac {T} {P} \ frac {V} {L} \ ge W $$

Rozważmy $ P $ i $ L $ jako zmienne i ustalmy $ T $ (zakładamy, że eksperyment wykonujemy w stałej temperaturze)

$$ V \ ge k_2 PL $$

Minimalne $ V $ wymagane do zobaczenia obserwowalnego prądu wynosi:

$$ V_ {min} = V _ {\ text {breakdown}} = V_ {B} = k_2PL $$